|
Олимпиада по математике 11 класс
|
|
| Egor | Дата: Суббота, 24.01.2015, 11:20 | Сообщение # 1 |
|
Лейтенант
Группа: Проверенные
Сообщений: 66
Награды: 0
Репутация: 0
Статус: Offline
| Всероссийская и районная олимпиада школьников по математике 11 класс с решениями и ответами

Школьный тур и школьный этап, олимпиадные задания 2015, 2016, 2017, 2018 учебного года
Математические олимпиады вы можете смотреть и решать онлайн, а также можно бесплатно скачать к себе на компьютер и решать в свободное время дома или в школе.
Авторы заданий: Дробышев, Кенгуру, Узорова, Нефедова, Белицкая, Орг, Балаян, Шевкин,
1 и 2 полугодие. Школа России. ФГОС
 Посмотреть и бесплатно скачать Ответы и Решения Олимпиады Посмотреть и бесплатно скачать Ответы и Решения Олимпиады
Задача 1 :
В игре участвуют два игрока А и Б. Игрок А задаёт значение одного из коэффициентов a, b или c многочлена
x3 + ax2 + bx + c.
Игрок Б указывает значение любого из двух оставшихся коэффициентов. Затем игрок А задаёт значение последнего коэффициента. Существует ли стратегия игрока А такая, что как бы ни играл игрок Б, уравнение
x3 + ax2 + bx + c = 0
имеет три различных (действительных) решения?
Задача 2 :
Пусть
f(x) = (...((x – 2)2 – 2)2 – 2)2... – 2)2
(здесь скобок ( ) – n штук). Найдитеf І(0)
Задача 3 :
Числа a , b и c таковы , что
a2 + b2 + c2 = 1.
Докажите, что
a4 + b4 + c4 + 2(ab2 + bc2 + ca2)2 Ј 1.
При каких a, b и c неравенство превращается в равенство?
Задача 4 :
Пусть прямая L перпендикулярна плоскости P. Три сферы попарно касаются друг друга так, что каждая сфера касается плоскости P и прямой L. Радиус большей сферы равен 1 . Найдите минимальный радиус наименьшей сферы.
Задача 5 :
На валютной бирже острова Удача продают динары (D), гульдены (G), реалы ® и талеры (T). Биржевые маклеры имеют право совершить сделку купли-продажи с любой парой валют не более одного раза за день. Курсы валют такие: D = 6G, D = 25R, D = 120 T, G = 4R, G = 21T, R = 5T. Например, запись D = 6G означает,что 1 динар можно купить за 6 гульденов (или 6 гульденов можно продать за 1 динар). Утром у маклера было 80 динаров, 100 гульденов, 100 реалов и 50400 талеров. Вечером у него было одинаковое число динаров и талеров. Каково максимальное значение этого числа?
Задача 6 :
Известно, что n-вершинник содержит внутри себя многогранник M с центром симметрии в некоторой точке Q и сам содержится в многограннике, гомотетичном M, с центром гомотетии в точке Q и коэффициентом k. Найдите наименьшее значение k, если
а) n = 4, b) n = 5
Задача 7 :
Докажите, что существуют арифметические прогрессии произвольной длины, состоящие из различных попарно взаимно простых натуральных чисел.
Задача 8 :
Докажите, что плоскость, делящая в одинаковом отношении площадь поверхности и объем описанного многогранника проходит через центр вписанной в этот многогранник сферы.
Задача 9 :
В треугольнике ABC угол A равен a, а угол B равен 2a. Окружность с центром в точке C радиуса CA пересекает прямую, содержащую биссектрису внешнего угла при вершине B в точках M и N. Найдите углы треугольника MAN.
|
| |
| |
| Egor | Дата: Суббота, 24.01.2015, 11:21 | Сообщение # 2 |
|
Лейтенант
Группа: Проверенные
Сообщений: 66
Награды: 0
Репутация: 0
Статус: Offline
| Задачи и задания олимпиад по математике 11 класс. Вариант 2
Олимпус - Зимняя, осенняя и весенняя сессия
Городской и муниципальный этап
1.
Найдите такое натуральное число k, что 2008! делится на 2007k, но не делится на 2008k. (Напомним, чтоn! = 1·2·3·4·… ·n).
2.
Может ли вершина параболы y = 4x2 – 4(a + 1)x + a лежать во второй координатной четверти при каком-нибудь значении а?
3.
(an) – арифметическая прогрессия с разностью 1. Известно, что S2008 - наименьшая среди всех Sn (меньше суммы первых n членов для любого другого значения n). Какие значения может принимать первый член прогрессии?
4.
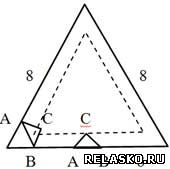
Внутри равностороннего треугольника со стороной 8 находится равнобедренный треугольник АВС, в котором АС = ВС = 1, ?С=120°. Две вершины А и В могут лежать либо на одной стороне большого треугольника, либо на двух. Где при этом может оказаться вершина тупого угла – точка С? Нарисуйте это геометрическое место точек и найдите длину соответствующей линии.
5.
Клетчатая прямоугольная сетка m x n связана из веревочек единичной длины. Двое делают ходы по очереди. За один ход можно разрезать (посередине) не разрезанную ранее единичную веревочку. Если не останется ни одного замкнутого веревочного контура, то игрок, сделавший последний ход, считается проигравшим. Кто из игроков победит при правильной игре и как он должен для этого играть?
6.
Докажите, что являются точными квадратами все числа вида 16, 1156, 111556 и т.д. (в середину предыдущего числа вставляется число 15).
7.
В пруд пустили 30 щук, которые постепенно поедали друг друга. Щука считается сытой, если она съела трёх щук (сытых или голодных). Каково наибольшее число щук, которые могут почувствовать себя сытыми за достаточно большой промежуток времени?
8.
Найдите, какую цифру обозначает каждая буква в следующем равенстве: АХА=БАХ.
9.
Двое пишут 30-значное число, употребляя только цифры 1, 2, 3, 4, 5. Первую цифру пишет первый, вторую --- второй, третью --- первый и т.д. Может ли второй добиться того, чтобы полученное число разделилось на 9, если первый стремится ему помешать?
10.
Можно ли замостить шашечную доску 10*10 плитками 4*1?
|
| |
| |
| Egor | Дата: Суббота, 24.01.2015, 11:21 | Сообщение # 3 |
|
Лейтенант
Группа: Проверенные
Сообщений: 66
Награды: 0
Репутация: 0
Статус: Offline
| Решение задач по математике 11 класс
1.
Разложим число 2007 на простые множители: 2007 = 32 ? 223.
В разложении на простые множители числа 2007! показатель степени у числа 3 будет достаточно большим, так как множитель 3 входит в разложение каждого третьего числа. Множитель 223 входит только в разложение чисел вида 223р, где р – натуральное число, не превосходящее 9. Таким образом, в разложение числа 2007! на простые множители число 223 войдет с показателем 9. Следовательно, число 2008! будет делиться на 2007k, где k=9.
2.
Координаты вершины параболы x0 = (a + 1)/2, y0 = 4((a + 1)/2)2 - 4(a +1)(a + 1)/2 + a = -a2 - a - 1 = -(a + 1/2)2 - 3/4. Так как у0 < 0 при любых значениях а, то во второй координатной четверти вершина параболы находиться не может.
3.
Так как разность прогрессия положительна, то прогрессия – возрастающая. Следовательно, описанная ситуация возможна тогда и только тогда, когда члены прогрессия с первого по 2008-ой – отрицательны, а начиная с 2009-го – положительны. Таким образом, S2008 будет наименьшей, тогда и только тогда, когда а2008 < 0, a2009 > 0. Отсюда получаем систему неравенств
4.
Если вершина А и В лежат на одной стороне треугольника, то вершина С лежит на отрезке прямой, параллельной этой стороне. Длина этого отрезка равна 8 - ?3. Пусть вершины А и В лежат на двух сторонах равностороннего треугольника с общей вершиной О. Тогда вокруг четырехугольника АСВО можно описать окружность (четырехугольник является вписанным). В этой окружности углы ВАС и ВОС равны, так как опираются на одну и ту же дугу с хордой ВС. Следовательно, угол ВОС равен 30°. Следовательно, третья вершина треугольника – точка С – лежит на биссектрисе угла равностороннего треугольника. Длина соответствующего отрезка биссектрисы равна 1. Итак, точка С может лежать на стороне некоторого равностороннего треугольника и на некоторых отрезках биссектрис внутренних углов этого треугольника. Длина шести звеньев этой линии равна 27 - 3?3.
5.
если m + n – четно, то выигрывает второй игрок, если m + n – нечетно, то выигрывает первый. В начале игры веревочек единичной длины было m(n + 1) + n(m + 1) = 2mn + m + n. Это число имеет ту же четность, что и число m + n. Последний ход в игре разрушает последний замкнутый контур. Докажем, что граница любого замкнутого конура содержит четное количество веревочек единичной длины. Действительно, рассмотрим границу произвольного замкнутого контура. Каждый вертикальный столбец исходной сетки содержит четное количество горизонтальных веревочек единичной длины из этой границы (возможно, и нулевое), т. к. войдя в замкнутый контур, например, снизу, мы обязаны из него выйти. Аналогично, каждая горизонтальная строка исходной сетки содержит четное количество вертикальных веревочек единичной длины. Таким образом, общее количество единичных веревочек на границе замкнутого контура – четно. Выигрышная стратегия для любого игрока состоит в том, чтобы не разрушать последний замкнутый контур, пока есть такая возможность.
|
| |
| |